③性差の検討
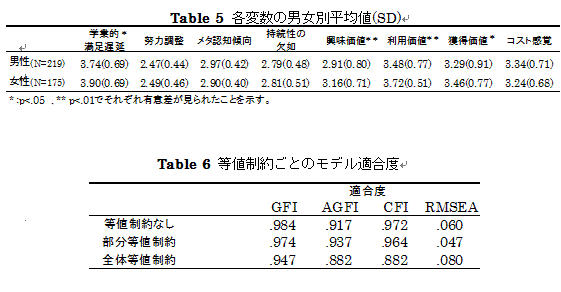
最後に、学業的満足遅延が男女共通の概念であるかを確認するために、性差についての分析を行った。まずは全ての変数に対し男女による平均値差を検討するため、Welchの方法を用いて平均値の差の検定を行った(Table 5)。学業的満足遅延(t(392)=2.20, p <.05)と興味価値(t(392)=3.29, p <.01)、獲得価値(t(378)=3.70, p <.01)、利用価値(t(390)=2.00, p <.05)に有意差がみられた。その他の変数に男女で有意差は見られなかったため、信頼区間を算出し変数の優劣を検討した結果、それらの平均値間に非劣性が確認された。
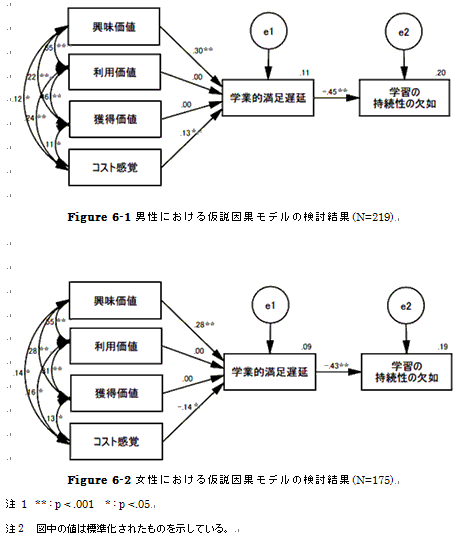
次に、先の結果から得られたモデルが男女によって異なるかどうかを検討するため、先ほどのモデルで多母集団同時分析を行った。手順は以下の通りである。
まず最初に、等値制約を設けず推定値の算出を行った。次に、推定値に男女で有意差が見られなかった興味価値と利用価値の間の共分散、利用価値と獲得価値から学業的満足遅延へのそれぞれのパス、学業的満足遅延から持続性の欠如へのパスに等値制約を設けた。なお、係数が0に等しかった利用価値と獲得価値からのパスには値が0であるという制約も加えた。これらの条件の下、再度分析を行った。最後に、全てのパスに等値制約を設けた分析を行い、それぞれのモデル適合度を比較した(Table 6)。
TOP