5.階層的重回帰分析による検討

　5．階層的重回帰分析による検討

　期待の程度・対人葛藤方略スタイルと教師の指導行動及びそれらの交互作用が教師からの期待の受け止め方にどのように影響を及ぼすかについて検討するために，階層的重回帰分析を行った。なお，多重共線性の問題を回避するため，用いるすべての変数を中心化し交互作用項を作成した。この分析を行うことで，従属変数への予測力が増加するのかを検討することができ，従属変数において有効な独立変数を明らかにすることが出来る。

　5-1． 対人葛藤方略スタイルが期待の程度と指導行動に及ぼす影響

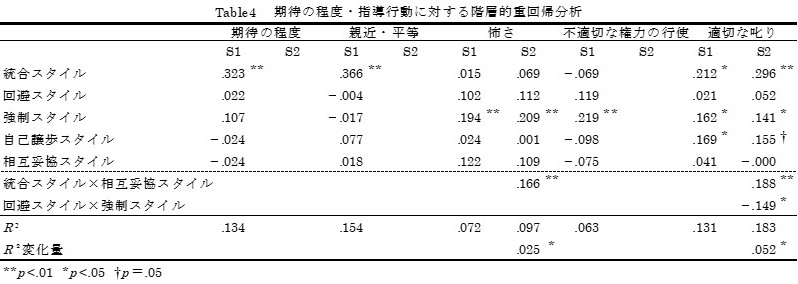
　対人葛藤方略スタイル及びその交互作用が期待の程度と教師の指導行動にどのように影響を及ぼしているのかを調べるため，対人葛藤方略スタイル及びその交互作用項を独立変数，期待の程度と教師の指導行動を従属変数として，階層的重回帰分析を行った。まず，第1ステップで対人葛藤方略スタイルを回帰式に強制投入法で投入した。続いて，第2ステップで対人葛藤方略スタイルの交互作用項をステップワイズ法で投入した。階層的重回帰分析の結果をTable4に示す。第2ステップで，交互作用項を投入すると，教師の指導行動のうち「怖さ」，「適切な叱り」において有意となった。

　「期待の程度」には「統合スタイル」から有意な正の影響がみられた（β＝.323；p＜.01）。「親近・平等」には「統合スタイル」から有意な正の影響がみられた（β＝.366；p＜.01）。「怖さ」には「強制スタイル」「統合スタイル×相互妥協スタイル」から有意な正の影響がみられた（順にβ＝.209；p＜.01，β＝.166；p＜.01）。「不適切な権力の行使」には「強制スタイル」から有意な正の影響がみられた（β＝.219；p＜.01）。「適切な叱り」には「統合スタイル」「強制スタイル」「統合スタイル×相互妥協スタイル」から有意な正の影響がみられた（順にβ＝.296：p＜.01，β＝.144；p＜.05，β＝.188；p＜.05）。そして，「回避スタイル×強制スタイル」から有意な負の影響がみられた（β＝−.149；p＜.05）。また，「自己譲歩スタイル」からの正の影響が有意傾向であった（β＝.188；p＝.05）。